[프로그래머스] Lv 2. 3 x n 타일링(Python)

코딩테스트 연습 - 3 x n 타일링

 

문제

가로 길이가 2이고, 세로의 길이가 1인 직사각형 모양의 타일이 있습니다.

이 직사각형 타일을 이용하여 세로의 길이가 3이고 가로의 길이가 n인 바닥을 가득 채우려고 합니다.

 

직사각형 가로의 길이 n이 매개변수로 주어질 때, 이 직사각형을 채우는 방법의 수를 return 하는 solution 함수를 완성해주세요.

 

풀이

경우의 수가 많은 걸 보니 dp를 이용해 풀 수 있을 거 같습니다.

먼저 문제 특성 상 n이 홀수일 때는 불가능하므로 n이 짝수일 때만 생각해보겠습니다.

 

n이 2일 때는 0에서 2칸을 채우는 방법만 가능하므로 경우의 수가 3개 입니다.

n이 4일 때는 2에서 2칸을 채우는 방법이 3개 이므로 총 9개(3*3) + 0에서 4개를 채우는 방법 2개 -> 11개의 방법이 있습니다.

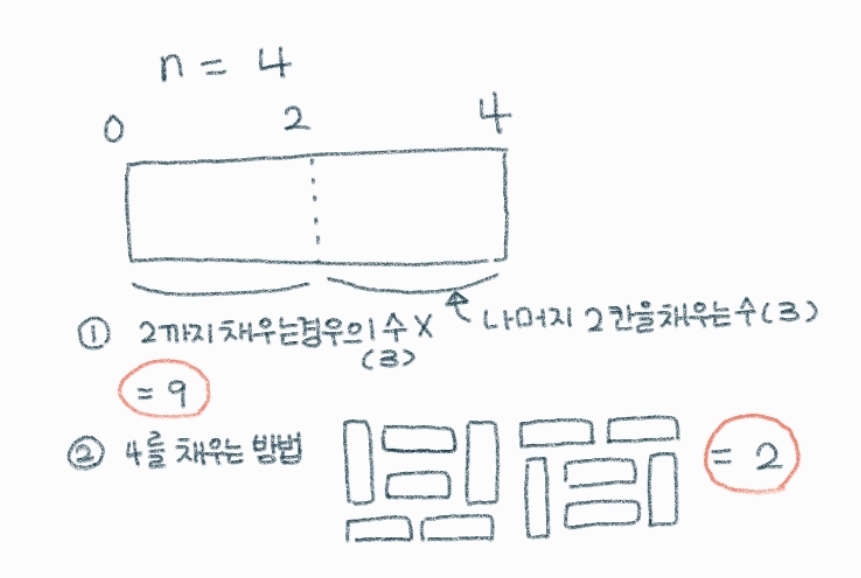
그럼 6개일 때는 몇 개의 방법으로 만들 수 있을까요?

1. 4에서 2칸을 채우는 방법은 4까지 만드는 방법 11개 * 2칸을 채우는 방법 3개 -> 33개

2. 2에서 4칸을 더 채우는 방법은 2까지 만드는 방법 3개 * 4칸을 채우는 방법 2개 -> 6개

3. 0에서 6칸을 채우는 방법은 2개

총 41개의 방법이 있습니다.

 

이렇게 쭉 계산하다보면 공식을 알 수 있습니다.

dp[i]의 값은

1. + dp[i-1]*3 ( 2칸을 더 채우는 방법 )

2. + dp[0]부터 dp[i-2]의 경우의 수 * 2 ( i부터 i-2 크기를 채우는 방법 )

🌹 2를 곱해주는 이유

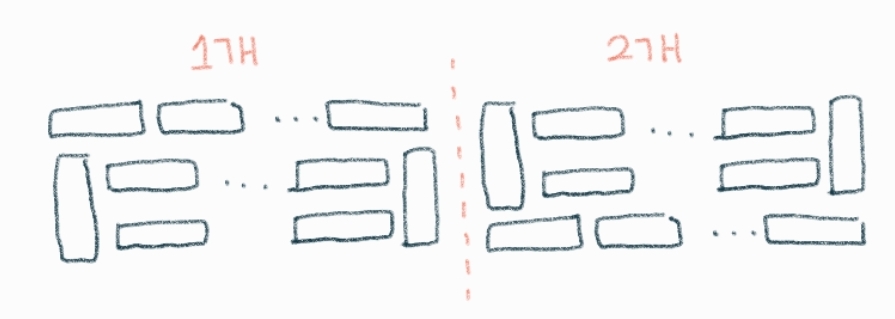
따라서, 아래 코드와 같이 dp를 작성할 수 있습니다.

dp[i] = (dp[i-1]*3 + h) % 1000000007​

🌹 h = dp[0] ~ dp[i-2]의 경우의 수 * 2

 

코드

def solution(n):
    dp = [0] * (n-(n//2-1))
    dp[0] = 1
    
    h = 0
    INF = 1000000007
    for i in range(1,n//2+1):
        dp[i] = (dp[i-1]*3 + h)%INF
        h += dp[i-1] * 2
    
    return dp[-1]